Explore Data Parallel C++ Usage Models from Intel® oneAPI Math Kernel Library
Alina Elizarova and Pavel Dyakov, math algorithm engineers,
and Gennady Fedorov, software technical consulting engineer, Intel Corporation
@IntelDevTools
Get the Latest on All Things CODE
Sign Up
Intel® oneAPI Math Kernel Library (oneMKL) gives developers and data scientists enhanced math routines for creating science, engineering, or financial applications. You can use it to optimize code for current and future generations of Intel® CPUs and GPUs. This article shows you how to apply Data Parallel C++ (DPC++) usage models from oneMKL to a Monte Carlo simulation using the oneMKL random number generators (RNG).
Let's look at five usage models:
- Reference C++
- oneMKL DPC++
- Extended oneMKL DPC++
- Heterogeneous parallel implementations
- Implementations based on different memory allocation techniques
The bottom line? Minimizing data transfer between the host and device significantly improves performance.
Compute π by Numerical Integration
Monte Carlo simulations are a broad class of computational algorithms that use repeated, random sampling to obtain numerical results1. Figure 1 shows how to compute π using the Monte Carlo method.

Figure 1. Compute π using the Monte Carlo method
Consider a quadrant inscribed in a unit square. The area of sector S is equal to Area(S)=1/4 πr2=π/4, and the area of the square R is equal to Area(R)=1. If we randomly choose the point c=(x,y) from the unit square R, the probability that c is within sector S is:
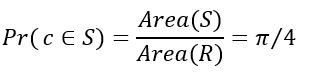
When considering n points, where n is sufficiently large, count the number of points falling into S – k. Then, we can approximate the probability ![]() by the ratio k/n, or:
by the ratio k/n, or:

We can approximate π as:

According to the laws of large numbers, the larger the n, the more accurate our π approximation. More accurately, from the Bernoulli theorem, for any ε>0:

If x and y coordinates of the tested point c are 0≤x≤1 and 0≤y≤1 (abscissa and ordinate, respectively), then c falls into sector S when:
x2+y2≤1
To summarize:
- Generate n 2D points where each point is represented by two uniformly distributed random numbers over the [0,1) interval.
- Count the number of points that fall into sector S.
- Calculate the approximate value of π using the previous formula.
Reference C++ Example of π Estimation
Consider a function estimate_pi that takes several 2D points n_points and performs the previously described computation:

This example uses RNG functionality from the C++ 11 standard. In Step 1, we initialize the RNG by creating two instances: engine and distribution. The engine holds a state of a generator and provides independent and identically distributed random variables. distr describes transforming generator output with statistics and parameters. In this example, uniform_real_distribution produces random floating-point values, uniformly distributed in the interval [a, b).
In Step 1.2, random numbers are obtained by passing the engine to an operator() distribution. A single floating-point variable is obtained. The loop fills vectors x and y with random numbers. In Step 2, each (x, y) position is checked to determine how many points fall into the S sector. The result is stored in the n_under_curve variable. Finally, the estimated π value is calculated and returned to the main program (Step 3).
oneMKL DPC++ Example of π Estimation
Now let's modify the previous estimate_pi function and add cl::sycl::queue. DPC++ lets you choose a device to run on using a selector interface:

cl::sycl::queue is an input argument to oneMKL functions. The library kernels are submitted in this queue with no code changes required to switch between devices (such as the host or accelerator). CPU and GPU devices are available in the oneMKL release.
Instead of std::vector, cl::sycl::buffer is used to store the random numbers:

Buffers manage data transfer between the host application and device kernels. The buffer and accessor classes are responsible for tracking memory transfers and guaranteeing data consistency across the different kernels.
In Step 1, the RNG APIs for oneMKL also initialize two entities (the RNG engine and random number distribution) as shown in Step 1.1, the engine takes cl::sycl::queue and an initial seed value as input to the constructor. The distribution mkl::rng::uniform has template parameters for the type of output values and method used to transform the engine output (for details, see Developer Reference) and distribution parameters.
The mkl::rng::generate function is called at Step 1.2 to obtain random numbers. This function takes the distribution and engine created in the previous step, the number of elements to be generated, and storage for the result in buffers. The RNG API for oneMKL mkl::rng::generate() is vectorized. Vector library subroutines often perform better than scalar routines (for details, see Intel® oneMKL Vector Statistics Notes).
In Step 2, the random numbers are postprocessed on the host. Host accessors for buffers are created to access the data:

Other steps are the same as in the C++ reference example.
Extended oneMKL DPC++ Example of π Estimation
We can optimize Step 2 in the previous example using the DPC++ Parallel STL function. This approach reduces data transfer between the host and device, which improves performance. The modification to Step 2 is as follows:

The zip iterator provides a pair of random numbers as input to the count_if function. Other steps are the same as in the previous oneMKL DPC++ example.
Example of a oneMKL DPC++ π Estimation Based on Unified Shared Memory (USM)
There are two approaches to DPC++ pointer-based memory management: cl::sycl::malloc and cl::sycl::usm_allocator (for more details, see GitHub*).
cl::sycl::malloc allows you to allocate memory directly on the host or device, or to access memory from both the host and device:

This memory allocation provides all the advantages of pointer arithmetic as well. This approach requires you to free any allocated memory.
The cl::sycl::usm_allocator approach allows you to work with standard or user containers without worrying about direct memory control:

Generation is performed in the same way, but instead of cl::sycl::buffer<float, 1>, float* is used:

Each function returns a cl::sycl::event that can be used for synchronization. You can call wait() or wait_and_throw() functions for these events or for the entire queue. This allows manual control of data dependencies between DPC++ kernels by calling event.wait() or queue.wait() functions.
To obtain random numbers and to count points in Step 2, you can use vectors and pointers without creating host accessors:

Heterogeneous Running of a oneMKL DPC++ π Estimation
You can modify the previous examples to offload part of the computation to an accelerator instead of doing the entire computation on the host. The APIs stay the same. You just need to choose the device for cl::sycl::queue. Two queues are needed for parallel running on different devices:

You can also allocate memory separately. CPU allocation can be done directly on the host:

You need to construct RNG engines in oneMKL for the exact type of device, so two objects are required. The second engine may be initialized with another seed or continue the sequence offset by n_points. (For details, see RNGs in parallel computations in the oneMKL Vector Statistics Notes.)

Generation and postprocessing may be called as in the previous examples. In this example, std::count_if is used on a host with a parallel running policy:

This approach allows balancing work between devices and completes different tasks in parallel on any supported devices within a single API.
Performance Comparison
Figure 2 compares the oneMKL DPC++ and Extended oneMKL DPC++ examples.

Figure 2. Performance comparison
The hardware and software parameters are:
- Hardware: Intel® Core™ i9-9900K processor at 3.60 GHz, 12th generation LP version of Intel® HD Graphics, NEO Graphics
- Operating system: Ubuntu* 18.04.2 LTS
- Software: oneMKL
Simulation parameters:
- Number of generated 2D points: 108
- Random number engine: mkl::rng::philox4x32x10
- Random number distribution: Uniform single-precision
- Measurement region: Computational part of estimate_pi() functions (without memory allocation overhead)
Conclusion
This article provided demonstrations of different oneMKL DPC++ usage models applied to π estimation by Monte Carlo simulations. Slightly modifying the reference C++ example lets you use DPC++ features and oneMKL functions to run code on the different supported devices, including heterogeneous running. Reducing data transfer between the host and device can significantly improve performance, as shown in Figure 2.
Reference
- Knuth, Donald E., Seminumerical Algorithms, vol. 2 of The Art of Computer Programming, 2nd edition. Reading, Massachusetts: Addison-Wesley Publishing Company, 1981.
______
You May Also Like
Get started with this core set of tools and libraries for developing high-performance,
data-centric applications across diverse architectures.
Get It Now
See All Tools