Loop blocking (also known as loop tiling) is one of the most effective optimization techniques from the long list of possible loop optimizations you can apply to your code. The general idea of this technique is to  change the loop’s iteration space into smaller blocks in order to work with the memory hierarchy more efficiently, i.e. we can guarantee that the data used in the loop will fit the cache until it is reused. We may significantly decrease the number of cache misses in this case and improve the performance of our application. Intel® compilers have a special directive forcing the compiler to use loop blocking optimization for the specified loop. But let’s start from the beginning.
change the loop’s iteration space into smaller blocks in order to work with the memory hierarchy more efficiently, i.e. we can guarantee that the data used in the loop will fit the cache until it is reused. We may significantly decrease the number of cache misses in this case and improve the performance of our application. Intel® compilers have a special directive forcing the compiler to use loop blocking optimization for the specified loop. But let’s start from the beginning.
MEMORY HIERARCHY
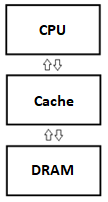 We all know that existing processors do have a cache - it is a small and fast memory located closer to a processor core and dedicated to minimizing an “expensive” access to DRAM. Note that cache is located between the processor and DRAM and keeps a copy of some data from main memory (DRAM).
We all know that existing processors do have a cache - it is a small and fast memory located closer to a processor core and dedicated to minimizing an “expensive” access to DRAM. Note that cache is located between the processor and DRAM and keeps a copy of some data from main memory (DRAM).
The cache is organized as a hierarchy of cache levels. Each cache level is larger and has longer latency than the previous one. The fastest and smallest is the level 1 cache (L1) which consists of data cache and instruction cache. L1 cache is checked first and, if it hits, then we don’t need to check the next cache levels. If that smaller cache misses, the next cache (L2) is checked, and so on. Note that highest-level cache (last cache checked before accessing main memory), also known as last level cache (LLC), is shared between cores.
Data access is performed by processor in blocks of small size called cache lines, so cache actually consists of many cache lines. The size of one cache line is 64 bytes. At least one cache line is copied from the memory to cache, if we try to read any data from memory. An access to any byte of data from the same cache line will be fast. If we access the data from a different cache line, then we will spend more time (still fast). However, a cache miss will result in a significant performance drop – we need to check all caches and, finally, fetch the data from main memory.
LOCALITY OF REFERENCE
We also need to talk about the important term, locality of reference. There are two basic types of reference locality - temporal and spatial. If a particular memory location is referenced, then it is likely that the same location will be referenced again quite soon. It is a temporal locality. If a particular storage location is referenced, then it is likely that nearby memory locations will be referenced soon. That is the reason why data is loaded from memory via 64 byte cache lines. There is one data element referenced in the code, however, we have a full line of data fetched and ready to use. If we work with data unit stride, then we implement a spatial locality.
Temporal locality in loops can be achieved by reusing the same data for multiple loop iterations. Loop blocking allows us to implement a temporal locality and guarantees that once the data is loaded to the cache it will be not evicted until it is used.
AN EXAMPLE
Let’s take a look on the following example
double A[MAX, MAX], B[MAX, MAX];
for (i=0; i< MAX; i++)
for (j=0; j< MAX; j++)
A[i,j] = A[i,j] + B[j, i];
For the first iteration of the inner loop, each access to array B will generate a cache miss. If the size of one row of array A, that is, A[2, 0:MAX-1], is large enough, by the time the second iteration starts, each access to array B will always generate a cache miss. For instance, on the first iteration, the cache line containing B[0, 0:7] will be brought in when B[0,0] is referenced, because the double-type variable is eight bytes, and each cache line is 64 bytes. Due to the limitation of cache capacity, this line will be evicted due to conflict misses before the inner loop reaches the end. For the next iteration of the outer loop, another cache miss will be generated while referencing B[0,1]. In this manner, a cache miss occurs when each element of array B is referenced, there is no data reuse from the cache at all for array B.
This situation can be avoided if the loop is blocked with respect to the cache size:
for (i=0; i< MAX; i+=block_size)
for (j=0; j< MAX; j+=block_size)
for (ii=i; ii<i+block_size; ii++)
for (jj=j; jj<j+block_size; jj++)
A[ii,jj] = A[ii,jj] + B[jj, ii];
As illustrated below, arrays A and B are blocked into smaller rectangular chunks so that the total size of two A and B chunks is smaller than the cache size. This allows maximum data reuse.
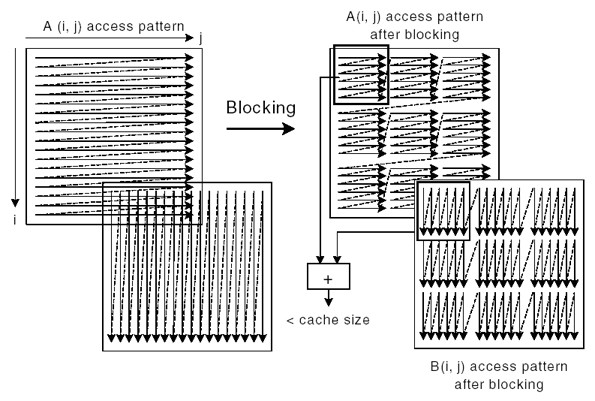
A block size is selected as the loop-blocking factor. Suppose that block size is eight; then the blocked chunk of each array will be eight cache lines (64 bytes each). In the first iteration of the inner loop, A[0, 0:7] and B[0, 0:7] will be brought into the cache. B[0, 0:7] will be completely consumed by the first iteration of the outer loop. Consequently, B[0, 0:7] will only experience one cache miss after applying loop blocking optimization, in lieu of, eight misses for the original algorithm..
As one can see, all the redundant cache misses can be eliminated by applying this loop blocking technique. If MAX is huge, loop blocking can also help reduce the penalty from DTLB (data translation look-aside buffer) misses. In addition to improving the cache/memory performance, this optimization technique also saves external bus bandwidth.Let’s compile a simple example and show how effective this technique may be.
#include <time.h>
#include <stdio.h>
#define MAX 8000
#define BS 16 //Block size is selected as the loop-blocking factor
void add(int a[][MAX], int b[][MAX]);
int main()
{
int i, j;
int A[MAX][MAX];
int B[MAX][MAX];
clock_t before, after;
//Initialize array
for (i=0; i<MAX; i++)
{
for(j=0;j<MAX; j++)
{
A[i][j]=j;
B[i][j]=j;
}
}
before = clock();
add(A, B);
add(A, B);
add(A, B);
add(A, B);
after = clock();
printf("\nTime taken to complete : %7.2lf secs\n", (float)(after - before)/ CLOCKS_PER_SEC); }
Function add performs the addition of the arrays.
First is the implementation with no loop blocking:
void add(int a[][MAX], int b[][MAX])
{
int i, j;
for(i=0;i<MAX;i++)
for(j=0; j<MAX;j++)
a[i][j] = a[i][j] + b[j][i];
}
Compiling this example on Windows* with Intel C++ compiler version 19.0 Update 1 with enough stack size (It is just a simple example to show an effect of blocking; you can easily change it to allocate the memory on heap):
icl /Qoption,link,"/STACK:1000000000" block.cpp
On a Skylake laptop it took 2.69 sec to run this application.
Let’s change the implementation of the add function to use a blocking technique:
void add(int a[][MAX], int b[][MAX])
{
int i, j, ii, jj;
for(i=0; i<MAX; i+=BS)
for(j=0; j<MAX; j+=BS)
for(ii=i; ii<i+BS; ii++)
for(jj=j; jj<j+BS; jj++) //outer loop
//Array B experiences one cache miss for
//every iteration of outer loop
a[ii][jj] = a[ii][jj] + b[jj][ii];
}
Recompiling and running it, the execution time is just 0.45 sec. THAT is a significant performance gain!
The reason we talked about loop blocking is that in Intel compilers (starting with version 16.0) there is a special directive which may help you to avoid rewriting your loops with blocking. It is a BLOCK_LOOP directive:
C/C++
#pragma block_loop [clause[,clause]...]
#pragma noblock_loop
It enables loop blocking for the immediately following nested loops, so the compiler may do all the required blocking on its own. You can set the blocking factor and loop level (up to 8 nested loops) using corresponding clauses factor and level. If there is no level and factor clause, the blocking factor will be determined based on the processor type and memory access patterns and it will apply to all the levels in the nested loops following this pragma.
You can set different block size for different loop levels, e.g.
#pragma block_loop factor(256) level(1)
#pragma block_loop factor(512) level(2)
sets a block size equal to 256 for outer loop and block size equal to 512 for inner loop in case you have a nested loop.
Here is one more example:
#pragma block_loop factor(256) level(1:2)
for(j=1; j<n ; j++)
{
f = 0;
for(i=1; i<n; i++)
{
f = f + a[i] * b[i];
}
c[j] = c[j] + f;
}
Let’s go back to our example and modify the original implementation of the add function to simply use a #pragma block_loop directive.
void add(int a[][MAX], int b[][MAX])
{
int i, j;
#pragma block_loop
for(i=0;i<MAX;i++)
for(j=0; j<MAX;j++)
a[i][j] = a[i][j] + b[j][i];
}
Recompiling the code we found that the execution time is similar to the time gotten with the initial version. It is definitely something that was not expected! The root cause is that the Intel compiler set a default O2 optimization level and it doesn’t have loop blocking enabled. In order to enable the support of loop blocking optimizations, you need to set O3 level. Recompiling our example with explicit O3 optimization level set:
icl /O3 /Qoption,link,"/STACK:1000000000" block.cpp
The execution time is 0.45 sec now and it is an expected result – same as we got by doing loop blocking by changing the code. Note that we just used all default settings for blocking directive.
To see what blocking the compiler performed, look at the optimization report.
icl /O3 /Qopt-report-phase=loop /Qoption,link,"/STACK:1000000000" block.cpp
LOOP BEGIN at block.cpp(35,11)
remark #25460: No loop optimizations reported
LOOP BEGIN at block.cpp(35,11)
remark #25460: No loop optimizations reported
LOOP BEGIN at block.cpp(35,11)
remark #25442: blocked by 16 (pre-vector)
LOOP BEGIN at block.cpp(36,12)
remark #25442: blocked by 129 (pre-vector)
LOOP END
LOOP END
LOOP END
LOOP END
By the way, we have made one more test and recompiled the code with O3 and no directive. The compiler didn’t apply any loop blocking in that case and I had slow performance again due to cache misses.
FORTRAN USERS
The BLOCK_LOOP directive works just fine for Fortran, too. Just remember that the memory layout is different for Fortran multi-dimensional arrays. Fortran is row-major order. C/C++ is column-major.
Fortran
!DIR$ BLOCK_LOOP [clause[[,] clause]...]
!DIR$ NOBLOCK_LOOP
CASES WHERE BLOCK_LOOP DIRECTIVE IGNORED
There are cases where the BLOCK_LOOP directive is not applied. A comment is written to the optimization report with the information.
- Iteration count in the loop to be blocked depends on outer loop index. Triangular loops are not supported and, in general, loop upper bound should be invariant with regard to whole loop nest.
- Loop to be blocked index is increased in non-linear way like doubling of index on each iteration. Loop is not recognized as counted loop (unknown or multi-exit).
- Directive BLOCK_LOOP may be ignored when there is an additional inner loop directive, like SIMD.
- Presence of intermediate instructions between loop headers to be blocked. The loop nest should be perfect
// Example of a perfect loop nest
for ()
for ()
// Example of a loop next that is not perfect
for()
some_code;
for()
- Loop nest too deep, greater than 3 levels.
- Structural restrictions: GOTOs are prohibited, only calls, if-statements and assignments are allowed.
- There is check to determine that the loop is good for fusion. In that case, blocking is disabled.
- The blocking factors can only be constants.
- The compiler option, -fp-model precise, disables the BLOCK_LOOP directive.
WHEN SHOULD LOOP BLOCKING BE CONSIDERED?
The user applies their knowledge of the code and algorithms used. Much research has been done for stencil and matrix multiplication codes that show good results for blocking those loops.
The dynamic analysis tools like Intel Advisor, specifically with its Integrated Roofline preview feature, or VTune™ Amplifier with its memory analysis are able to pinpoint bottle-necked cache levels more precisely for giving the user an idea about blocking factors or loop positions in the loop nest to be blocked. The memory access pattern analysis tools like in Intel Advisor may give even more insights about the behavior of this code with a specific level of cache (misses, evictions, utilization of cache lines, strides when accessing the arrays).
SUMMARY
The BLOCK_LOOP directive enables the compiler to automatically block a loop for effective cache usage. The directive is only enabled when optimization level O3 is specified. There are cases where the BLOCK_LOOP directive is not applied. Read the comments in the optimization report for the impact on your code.
REFERENCES
Intel Fortran Compiler Developer Guide and Reference, BLOCK_LOOP and NOBLOCK_LOOP
Intel C++ Compiler Developer Guide and Reference, BLOCK_LOOP and NOBLOCK_LOOP
As of December 2018
Wikipedia, Loop Nest Optimization
Wikipedia, Row- and Column-Major Order
"