| File(s): | GitHub |
| License: | MIT |
| Optimized for... | |
|---|---|
| Software: (Programming Language, tool, IDE, Framework) |
Intel® oneAPI DPC++/C++ Compiler |
| Prerequisites: | Familiarity with C++ and DPC++ |
This tutorial with code examples is an Intel® oneAPI DPC++ Compiler implementation of a two-dimensional finite-difference stencil that solves the 2D acoustic isotropic wave-equation. It illustrates the basics of the DPC++ programming language using direct programming.
Requirements
C++ programming experience and familiarity with the DPC++ basics are assumed. If you do not have prior exposure to DPC++, read the DPC++ resources listed at the end of this tutorial.
Introduction
In this tutorial, we chose the problem of solving a Partial Differential Equation (PDE), using a finite-difference method, to illustrate the essential elements of the DPC++ programming language: queues, buffers/accessors, and kernels (code is available on GitHub*). Use it as an entry point to start programming in DPC++ or as a proxy to develop or better understand complicated code for similar problems (For example, a more complex DPC++ code sample implementing a 16th order finite-difference stencil for the 3D isotropic wave equation is available on GitHub).
Many physical phenomena can be described by PDEs. One example is the wave equation, which describes waves propagating through a medium with specific characteristics (for example, isotropic or anisotropic, constant or variable density, and so on).
Finite-difference methods are used to approximate the solution of PDEs by approximating the continuous PDEs by a set of discrete difference equations, which can be solved iteratively in a computer.
Other examples of PDEs that can be solved by finite-difference methods include option pricing (in mathematical finance), Maxwell’s equations (in computational electromagnetics), the Navier-Stokes equation (in computational fluid dynamics) and others. The simple parallel finite-difference method used in this example can be easily modified to solve problems in the above areas.
This tutorial provides a DPC++ code sample that implements the solution to the wave equation for a 2D acoustic isotropic medium with constant density. This wave equation is solved using the finite-difference method (a 2nd order stencil) with the purpose of modeling wave propagation in the medium. This is useful in several disciplines, including earthquake and oil exploration seismology, ocean acoustics, radar imaging, nondestructive evaluation, and others.1
Problem Statement
If the medium is acoustic and its density is constant, the wave equation (PDE describing wave propagation in the medium) is:
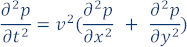
where p is the pressure, v is the medium velocity (velocity at which acoustic waves propagate in the medium), x and y are the two Cartesian coordinates, and t is the time. The wave can be initiated using initial conditions, defined by p at t=0, or using an explicit source function s(x,y). This code sample uses an explicit source function.
To obtain an approximate solution to this problem, we divide the model into a grid of N by N points (for simplicity we use a square grid, but a rectangular grid can be used). If we call ∆x, ∆y the distance between points in the grid in the x and y axes, respectively, and if ∆t is the increment in time (where time iterations range from n=0 to a defined maximum number of iterations), then by approximating the continuous partial derivatives using 2nd order central differences, we obtain the discretized equation:
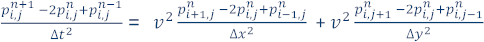
And solving for  (the value of the pressure wavefield at position i,j at time n+1), we can now describe a finite-difference formula to approximate the solution of the 2D acoustic wave equation:
(the value of the pressure wavefield at position i,j at time n+1), we can now describe a finite-difference formula to approximate the solution of the 2D acoustic wave equation:
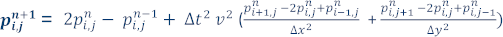
This is an explicit formula for the values of the pressure wavefield at time n+1 (at every point in the grid) based on the values of the pressure wavefield at time n and n-1.
Parallel Implementation and Code Sample Walk-Through
Grids used to represent models in finite-difference computations are natural candidates for simple domain-decomposition techniques because of their regularity. This is especially evident in the explicit finite-difference scheme shown here. It can be finely partitioned to expose the maximum possible concurrency—defining a task for each grid point because there are no data dependencies when computing the wavefield at different grid points for a given time step. Every point in the grid can be updated independently at every time iteration because the only data dependencies are on neighboring grid points at previous time steps, which are read-only.
At each time iteration, each point in the 2D grid can be updated according to the explicit formula shown above, as depicted in the following graphic representation of the stencil, where the updated value for the pressure wavefield is orange, and the neighboring grid points used for the update are green:
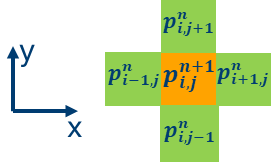
In this code sample, the update is included in the iso_2dfd_iteration_global function:
// Stencil code to update grid point at position given by global id (gid)
// New time step for grid point is computed based on the values of the
// the immediate neighbors in both the horizontal and vertical
// directions, as well as the value of grid point at a previous time step
value = 0.0;
value += prev[gid + 1] - 2.0*prev[gid] + prev[gid-1];
value += prev[gid + nCols] - 2.0*prev[gid] + prev[gid - nCols];
value *= dtDIVdxy * vel[gid];
next[gid] = 2.0f*prev[gid] - next[gid] + value;
Because this is the core part of the kernel function defined in this code sample, we explain how this stencil computation is constructed.
main() Function
First, look at the main function. Four one-dimensional arrays are defined and allocated:
int main(int argc, char* argv[]) {
float* prev_base;
float* next_base;
float* next_cpu;
float* vel_base;
Three of these arrays are used to update the wavefield in the kernel function: prev_base and next_base represent the pressure wavefield at iterations n and n+1, respectively. vel_base stores the medium velocity. The next_cpu array is equivalent to the next_base array, and it validates the computation in the device compared to the same computation performed in the host.
These arrays are allocated and passed as parameters to the initialize function, which initializes the wavefield arrays and velocity array, and adds the source function to the prev_base array. The source function used here is a discretized Ricker wavelet, commonly used in seismic data processing:
//Initialize arrays and introduce initial conditions (source)
initialize(prev_base, next_base, vel_base, nRows, nCols);
DPC++ Device Selector, Queues and Buffers
So far, this is standard C++ code. We start using DPC++ functionality when we create a device queue, which is used to enqueue work that will be executed in a particular device or accelerator, specified by the device_selector object:
// Define device selector as 'host', 'GPU' or 'default'
gpu_selector device_selector;
// default_selector device_selector;
// Create a device queue
queue q(device_selector, [&](exception_list eL) {
We can create device queues that will send work to specific devices. For example, we can use a GPU selector to enqueue work in a GPU, as shown here, or we can use a default selector, which would select a device at run-time.
The next step is to create buffer objects that communicate data between the host and the device. The buffers can store collections of elements that can be one, two, or three dimensional. In this case, we use them to store 1D arrays of floats (we use 1D arrays to represent 2D grids). Buffers are directly connected to how C or C++ stores arrays, so we connect them to the three arrays that are used in the pressure wavefield update calculation. Data in these buffers can be communicated back and forth between host and device:
buffer<float, 1> b_next(next_base, range<1>{nsize});
buffer<float, 1> b_prev(prev_base, range<1>{nsize});
buffer<float, 1> b_vel(vel_base, range<1>{nsize});
This shows that one buffer is declared for every float array, and the size of the buffer is specified by a 1D range of nsize elements:
// Compute the total size of grid
size_t nsize = nRows * nCols;
Command Handler and Kernel Definition
At this point, we want to create a loop that will iterate over time steps. This loop will update the value of the pressure wavefield at every grid point:
// Iterate over time steps
for (unsigned int k = 0; k < nIterations; k += 1){
// Submit command group for execution
q.submit([&](handler &cgh) {
At every time iteration, notice that we submit a command group to the device queue created above. The command group includes the kernel function that will be enqueued to the device defined in the queue.
This command group takes as a parameter a cgh command group handler, which is constructed at run-time and includes all the requirements for a kernel to execute. In this case, it’s in the GPU because we created a device queue with a GPU selector in the previous step.
Also, in a previous step, we created buffers in the host to hold data that we want to share between the host and the device. Now we create accessors to access data from the buffers in the device. These accessors act like pointers to memory objects that can be used in the device and are used in kernel functions to communicate data from and to the host, via the buffers that were defined above:
auto next = b_next.get_access<access::mode::read_write>(cgh);
auto prev = b_prev.get_access<access::mode::read_write>(cgh);
auto vel = b_vel.get_access<access::mode::read>(cgh);
Notice that the access mode of the accessors is both read and write for the buffers used to propagate the wavefield (b_next and b_prev) because these buffers are updated at every time step.
The next step is to define the execution range for the kernel function. In this example, we use a two-dimensional range which lets us define a collection of work items (executing instances of the kernel function) and every work item will execute an instance of the kernel function.
The example uses the grid size (given by input arguments nRows and nCols) to define the range:
auto global_range = range<2> (nRows, nCols);
Each work item in the range is now identified by a value of type item<2>, as shown in the next code snippet, where we send work to the device for execution. In DPC++, we can use the parallel_for function to send a kernel function to execute on the device. This kernel function is constructed using C++ lambda functions syntax. In C++ 11 and later, a lambda expression, like the one shown here, is a way of defining a function object at the location where it is invoked.
This parallel_for function creates a number of instances of the kernel function (specified by the global range and local range) and adds them to the command queue to be executed in parallel in the device:
cgh.parallel_for<class iso_2dfd_kernel>(
range<2>{global_range, [=](item<2> it) {
iso_2dfd_iteration_global(it, next.get_pointer(),
prev.get_pointer(), vel.get_pointer(),
dtDIVdxy, nRows, nCols);
});
The first parameter in the parallel_for function defines the range over which the kernel function will be executed, which is given by the global range. The second parameter of type item<2> is an index or an ID for each kernel invocation. This parameter ensures that every instance of the kernel executing in the device has a unique identifier. Also, the template parameter <class iso_2dfd_kernel> is used here to link the kernel and the host code. We need to add a class name here because the kernel is defined using C++ lambda functions syntax, and in C++, lambda functions do not have a name that can be used to link the kernel to the host code.
In the code snippet above, the body of the kernel function defines the code that will be executed in parallel by every instance of the kernel function created by the parallel_for function; in this case it’s the invocation of the iso_2dfd_iteration_global() function. This function updates the pressure wavefield at the grid point specified by the parameter it, which uniquely identifies (indexes) the instance of the kernel function executing in the device.
Before we discuss the iso_2dfd_iteration_global() function, it is important to know why the code contains an if-else statement that effectively swaps the next and prev pointers at every iteration:
if (k % 2 == 0)
cgh.parallel_for<class iso_2dfd_kernel>(
range<2>{global_range}, [=](item<2> it) {
iso_2dfd_iteration_global(it, next.get_pointer(),
prev.get_pointer(), vel.get_pointer(),
dtDIVdxy, nRows, nCols);
});
else
cgh.parallel_for<class iso_2dfd_kernel_2>(
range<2>{global_range}, [=](item<2> it) {
iso_2dfd_iteration_global(it, prev.get_pointer(),
next.get_pointer(), vel.get_pointer(),
dtDIVdxy, nRows, nCols);
});
This is so two arrays can be used for the update instead of three. By swapping the arrays at every iteration, we do not need to allocate a third array to hold the pressure wavefield at time  because that information can be read from the array that is about to be updated with the wavefield at time
because that information can be read from the array that is about to be updated with the wavefield at time  .
.
The iso_2dfd_iteration_global() function updates the pressure wavefield at the grid point specified by the parameter it. In this function, see how the local and global indices can be extracted from the parameter it (which is of type item<2>):
void iso_2dfd_iteration_global(item<2> it, float *next, float *prev,
float *vel, const float dtDIVdxy, int nRows,
int nCols) {
float value = 0.0;
// Compute global id
// We can use the get.global.id() function of the item variable to
// compute global id. The 2D array is laid out in memory in row major
// order.
size_t gidRow = it.get_id(0);
size_t gidCol = it.get_id(1);
size_t gid = (gidRow)*nCols + gidCol;
The computation of the global ID (gid) can be performed in several ways. The above code snippet shows one possible way and uses member functions of the item class.
The final step is to revisit the stencil computation. Using an if statement in the code snippet below, we first need to check that the update computation does not happen in the border of the array. The finite-difference stencil here uses the values of neighboring grid points to update a single grid point. Therefore, it is necessary to check that grid points in the border of the array (the ‘halo’) are not being updated to avoid segmentation faults. Notice that the constant HALF_LENGTH stores half of the stencil size (which is 2 in this case).
The computation to update a grid point is done using the value of the gid variable as an index. You can see how this is a fine-grain domain decomposition as every instance of the kernel function will update one point in the grid:
// Computation to solve wave equation in 2D
// First check if gid is inside the effective grid (not in halo)
if ((gidCol >= HALF_LENGTH && gidCol < nCols - HALF_LENGTH) &&
(gidRow >= HALF_LENGTH && gidRow < nRows - HALF_LENGTH) )
{
// Stencil code to update grid point at position given by global id (gid)
// New time step for grid point is computed based on the values of the
// the immediate neighbors in both the horizontal and vertical
// directions, as well as the value of grid point at a previous time step
value = 0.0;
value += prev[gid + 1] - 2.0*prev[gid] + prev[gid-1];
value += prev[gid + nCols] - 2.0*prev[gid] + prev[gid - nCols];
value *= dtDIVdxy * vel[gid];
next[gid] = 2.0f*prev[gid] - next[gid] + value;
}
The code walk-through is complete.
You can download the complete code sample by clicking the link at the top of the article. Note that this code sample is for educational purposes only; it is not optimized so that the use of DPC++ basic structures can be explicitly shown. This code is intended to provide a basic understanding of DPC++ and can be used as a starting point for more code development in DPC++.
Compiling and Running the Code
To compile and execute the code in Linux*, you configure the environment for Intel oneAPI. For example:
source <oneAPI install dir>/setvars.sh
In the directory where the code sample resides, type
mkdir build
cd build
cmake ..
make -j
To run the executable type
make run
Which will run the executable with pre-selected parameters.
You can also execute the code with different parameters as follows:
./iso2dfd 1000 1000 2000
The last command above will run the iso2dfd executable using a 1000x1000 grid size and it will iterate over 2000 time steps.
The execution above assumes that an Intel® Processor Graphics Gen9 is present in the system. If this is not the case, you can change the device_selector declaration in the code to a default_selector, which will use the CPU as a device if a GPU is not present:
//gpu_selector device_selector;
default_selector device_selector;
The output for the previous execution looks like the wavefield shown in the following figure. It shows a circular wavefront propagating from a source in the middle of the square grid. It was plotted using the output of iso2dfd using the SU Seismic processing library, which has utilities to display seismic wavefields and can be downloaded from John Stockwell’s SeisUnix GitHub* archive.

The following figure shows another example output. In this case we define a two-layer model (where the upper portion of the model has an acoustic wave speed of 3000 m/s, and the bottom portion has a speed of 1500 m/s, as shown in the left portion of the figure) and run the code several times varying the total number of time iterations. In this way we can get snapshots of how the wave (and its reflections and refractions at the edges of the model and at the interface between the two layers) are propagating in time through both the fast and slow portions of the model.

Summary
This tutorial describes a parallel implementation of a two-dimensional finite-difference stencil that solves the 2D acoustic isotropic wave-equation. The complete code sample is available to download from GitHub and is intended to show the the basic elements of the DPC++ programming language in a simple yet real-world application. Use it as a starting point for developing more complex applications. In particular, it can help you understand more complex finite-difference stencil parallel codes, like the 3D, 16th order stencil cited in the Resources section.
Resources
The Intel® oneAPI Toolkits site has detailed descriptions of DPC++ and oneAPI toolkits.
For more documentation and code samples, see Featured Documentation on the Intel® oneAPI Toolkits site.
The ISO3DFD DPC++ code sample is a more sophisticated solution to a 3D isotropic wave propagation problem using a 16th order stencil.
References
- Villarreal, A., & Scales, J. A. (1997). Distributed three-dimensional finite-difference modeling of wave propagation in acoustic media. Computers in Physics, 11, 388.